【量子機械学習】量子ニューラルネットワーク（ディープラーニング）の最急降下法の話。

目次。

目次。
はじめに。
読んだ論文。
- 題名。
- 著者。
量子ニューラルネットワーク。
さいごに。

この文章を読んで、面白い！役に立った！...と思った分だけ、投げ銭していただけると嬉しいです。

【宣伝】ギターも歌も下手だけど、弾き語りをやっているので、よければ聴いてください。

www.youtube.com

はじめに。

2022年のノーベル物理学賞は、「量子もつれ光子対を用いた、ベルの不等式の破れの実験的検証。ならびに量子情報科学の開拓」だった。量子情報科学分野のノーベル賞受賞は、初めてのことなので、それに触発されて、何かしら量子情報科学関連の文章を書くことにした。

以前から、量子敵対的生成ネットワークを解説する文章を書きたいと思っていたが、それには、量子コンピュータ上での最急降下法の知識が必要。

ということで、まずは量子コンピュータ上での最急降下法の話をする。量子敵対的生成ネットワークの解説は、時間とやる気があれば、今後するかも。

一般向けではないので、ご容赦ください。量子情報科学の本を読みとおすことができれば、この文章も読めると思います。そして、この本を読めば、2022年のノーベル物理学賞のことがよくわかります。

posted with カエレバ

「高校数学の知識がない人が量子情報科学の論文が読めるようになるために、どういう本を読めばいいか」というのを以下の文章の最後の方に書いたので、よければどうぞ。

blog.sun-ek2.com

量子コンピュータ上での最急降下法の論文も量子敵対生成ネットワークの論文も、以下の文章で紹介しているので、よければ。

blog.sun-ek2.com

==========

ちょくちょく宣伝しているが、新型コロナウイルスの論文を使って、「研究者がどうやって未知のウイルスの正体を暴くのか？」について説明した文章を一般の人向けに書いたので興味のある方はどうぞ。
blog.sun-ek2.com

加えて、PCR検査の仕組みと、それに代わるかもしれないゲノム編集技術を応用した新しい検査方法に関する論文を一般向けに説明したので興味のある方はどうぞ。
blog.sun-ek2.com

さらに、試験管内で新型コロナウイルスのスパイクタンパク質を進化させて、色々な変異体を取ってきたという論文を一般向けに説明したので興味のある方はどうぞ。

blog.sun-ek2.com

==========

読んだ論文。

題名。

Classification with Quantum Neural Networks on Near Term Processors

arxiv.org

著者。

Edward Farhi, Hartmut Neven

量子ニューラルネットワーク。

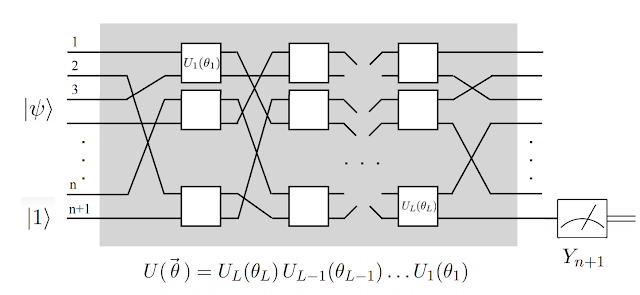
論文で扱っている量子ニューラルネットワークは、こんな感じ。

https://ai.googleblog.com/2018/12/exploring-quantum-neural-networks.htmlから引用。

L個の2量子ビットゲートに(z+1)量子ビットを入力する。z個の量子ビットは、入力データで、最後の1量子ビットは、最終出力を得るための量子ビット。

$\displaystyle U_{k}\left( \theta _{k}\right)=I \otimes … \otimes I \otimes U_{2 qubits}\left( \theta _{k}\right) \otimes I \otimes ... \otimes I$

$\displaystyle U\left( \vec{\theta}\right) =U_{L}\left( \theta _{L}\right)...U_{k}\left( \theta _{k}\right)...U_{1}\left( \theta _{1}\right)$

$\displaystyle | ψ_{output}\rangle = U\left( \vec{ \theta} \right) | z,1\rangle=U\left( \vec{\theta}\right) | ψ \rangle | 1\rangle$

量子ビット列の最後をYゲートに通して、測定すると、次のような期待値が得られる。

$\displaystyle\langle z,1| U^{†}\left( \vec{ \theta} \right) Y_{n+1}U\left( \vec{ \theta} \right) | z,1\rangle$

この期待値は、-1から1までの値のどれかを取る。これを教師データのラベルに一致させるように学習を行う。

ユニタリ変換を積み重ねるだけでは、厳密には、ニューラルネットワークとは言えない。

…ということも、一応、言及しておこうと思う。

厳密には、この量子ニューラルネットワークは、ニューラルネットワークではない。線形変換であるユニタリ変換を一億個、一兆個、一京個、積み重ねても、それは、ただ一つのユニタリ変換で表現されてしまう。ユニタリ変換でできたネットワークの層が一億層、一兆層、一京層、あったとしても、それは、一層と変わりがない。

これは、通常のニューラルネットワーク（ディープラーニング）でも同じこと。それぞれの層の出力は、非線形関数（シグモイド関数、ReLUなど）を通って出てくると思う。もし、ニューラルネットワークに線形関数しか使われてなければ、層をいくら重ねても、線形関数の性質より、全て一層に置き換えられる。

この問題は、量子ニューロンという技術で一応、解決することができる。以下のwebサイトの説明がわかりやすかったので、よければ。

qiita.com

ということも、一応、念頭に置いて、今後の文章を読んでください。

誤差関数（目的関数）。

誤差関数は、次の通り。

$\displaystyle loss\left( \vec{\theta}, z\right) = 1-l\left(z\right)\langle z,1| U^{†}\left( \vec{ \theta} \right) Y_{n+1}U\left( \vec{ \theta} \right) | z,1\rangle$

$\displaystyle l\left(z\right)$ は、教師データのラベル。誤差関数は、出力の期待値と教師データのラベルが一致すれば、0になり、一致しなければ、1となる。

パウリ行列 $\displaystyle \left\{ \sigma_{x} , \sigma_{y} , \sigma_{z} \right\}$ のテンソル積を $\displaystyle \Sigma_{k}$ とおくと、 $\displaystyle U_{k}\left( \theta _{k}\right)$ は、次のように書くことができる。

$\displaystyle U_{k}\left( \theta _{k}\right)=exp\left(i{ \theta_k}\Sigma_{k}\right)$

ユニタリ行列がエルミート行列の行列指数関数になる理由は、以下のwebサイトを参照のこと。

risalc.info

任意のエルミート行列がパウリ行列で展開できる理由は、以下のwebサイトを参照のこと。

electrodynamics.hatenablog.com

$\displaystyle U_{k}\left( \theta _{k}\right)=exp\left(i{ \theta_k}\Sigma_{k}\right)$ であることを念頭に、 $\displaystyle loss\left( \vec{\theta}, z\right)$ を $\displaystyle \theta_{k}$ で偏微分すると、

$\displaystyle\frac{\partial}{\partial \theta_{k}}loss\left( \vec{\theta}, z\right)$

$\displaystyle= i l\left(z\right) \langle z,1| U^{†}_{1}...U^{†}_{k}\Sigma^{†}_{k}...U^{†}_{L} Y_{n+1}U_{L}...U_{k}...U_{1} | z,1\rangle$

$\displaystyle -i l\left(z\right) \langle z,1| U^{†}_{1}...U^{†}_{k}...U^{†}_{L} Y_{n+1}U_{L}...\Sigma_{k}U_{k}...U_{1} | z,1\rangle$

複素関数の内積の公式 $\displaystyle \langle x| \left(AB...YZ \right)^{†} | y \rangle = \left( \langle y | \left( ZY...BA \right) | x \rangle \right)^{*}$ を使うと、

$\displaystyle \frac{\partial}{\partial \theta_{k}}loss\left( \vec{\theta}, z\right)$

$\displaystyle= i l\left(z\right) \left( \langle z,1| U^{†}_{1}...U^{†}_{k}...U^{†}_{L} Y_{n+1}U_{L}...\Sigma_{k}U_{k}...U_{1} | z,1\rangle\right)^{*}$

$\displaystyle -i l\left(z\right) \langle z,1| U^{†}_{1}...U^{†}_{k}...U^{†}_{L} Y_{n+1}U_{L}...\Sigma_{k}U_{k}...U_{1} | z,1\rangle$

$\displaystyle =2l\left(z\right)Im\left(\langle z,1| U^{†}_{1}...U^{†}_{k}...U^{†}_{L} Y_{n+1}U_{L}...\Sigma_{k}U_{k}...U_{1} | z,1\rangle\right)$

*論文の式（23）は、 $\displaystyle l\left(z\right)$ がないが、僕はつけた方がいいと思う。

$\displaystyle =Im\left(\right)$ は、虚部（a+ibのbの部分）を表す。複素共役の引き算なので、実部が消え、純虚数となる。そこにiがかかるので、最終的な答えは実数になる。

演算子が長ったらしいので、以下のように書き換える。

$\displaystyle 𝓤 \left( \vec{\theta} \right)=U^{†}_{1}...U^{†}_{k}...U^{†}_{L} Y_{n+1}U^{†}_{1}...\Sigma_{k}U_{k}...U_{L}$

$\displaystyle loss\left( \vec{\theta}, z\right)$ を $\displaystyle \theta_{k}$ で偏微分すると、

$\displaystyle \frac{\partial}{\partial \theta_{k}}loss\left( \vec{\theta}, z\right)= 2l\left(z\right)Im\left(\langle z,1| 𝓤\left( \vec{\theta}\right) | z,1\rangle\right)$

誤差関数の偏微分を量子回路で求める。

補助量子ビットを用意し、アダマール変換を行う。

$\displaystyle | ψ_{1}\rangle=| z,1 \rangle \otimes H | 0 \rangle$

$\displaystyle = \frac{1}{\sqrt{2}} | z,1 \rangle \left( | 0 \rangle + | 1 \rangle \right)$

補助量子ビットを制御量子ビットとし、制御ユニタリ変換を行う。

$\displaystyle | ψ_{2}\rangle=\frac{1}{\sqrt{2}}\left( | z,1\rangle |0\rangle + i𝓤\left( \vec{\theta}\right)| z,1\rangle |1\rangle\right)$

補助量子ビットにさらにアダマール変換を行う。

$\displaystyle | ψ_{3}\rangle=\frac{1}{\sqrt{2}}\left( | z,1\rangle \otimes H |0\rangle + i𝓤\left( \vec{\theta}\right)| z,1\rangle \otimes H |1\rangle\right)$

$\displaystyle \frac{1}{2}\left( | z,1\rangle + i𝓤\left( \vec{\theta}\right)| z,1\rangle \right) |0\rangle + \frac{1}{2}\left( | z,1\rangle - i𝓤\left( \vec{\theta}\right)| z,1\rangle \right) |1\rangle$

*論文の式（28）と違うが、流石にこれは僕の方が正しいと思う。

$\displaystyle | ψ_{3}\rangle$ を次のようにおく。

$\displaystyle | ψ_{3}\rangle= | φ_{1}\rangle + | φ_{2}\rangle$

補助量子ビットを測定し、0がでる確率は、

$\displaystyle \langle φ_{1} | ψ_{3}\rangle= \langle φ_{1} | φ_{1}\rangle + \langle φ_{1} | φ_{2}\rangle = \langle φ_{1} | φ_{1}\rangle$

$\displaystyle = \frac{1}{4} \left( \langle z,1| - i \langle z,1| 𝓤^{†}\left( \vec{\theta}\right) \right) \left( | z,1\rangle + i𝓤\left( \vec{\theta}\right)| z,1\rangle \right) \langle 0|0\rangle$

$\displaystyle = \frac{1}{4} \left(\langle z,1| z,1\rangle +\langle z,1|𝓤^{†}\left( \vec{\theta}\right)𝓤\left( \vec{\theta}\right) | z,1\rangle \right)$

$\displaystyle -\frac{1}{4} i \left(\langle z,1|𝓤^{†}\left( \vec{\theta}\right) | z,1\rangle - \langle z,1|𝓤\left( \vec{\theta}\right) | z,1\rangle \right)$

$\displaystyle = \frac{1}{2} - \frac{1}{4} i \left\{ \left(\langle z,1|𝓤 \left( \vec{\theta}\right) | z,1\rangle\right)^{*} - \langle z,1|𝓤\left( \vec{\theta}\right) | z,1\rangle \right\}$

$\displaystyle =\frac{1}{2} - \frac{1}{2} Im\left( \langle z,1|𝓤\left( \vec{\theta}\right)| z,1\rangle \right)$

よって、

$\displaystyle \frac{\partial}{\partial \theta_{k}}loss\left( \vec{\theta}, z\right)= 2 l\left(z\right) Im\left( \langle z,1|𝓤\left( \vec{\theta}\right)| z,1\rangle \right) = l\left(z\right) \left( 2-4\langle φ_{1} | ψ_{3}\rangle \right)$

最急降下法。

ここまで求めることができれば、あとは普通のニューラルネットワーク（ディープラーニング）の最急降下法と変わらない。

$\displaystyle \vec{g}=\nabla loss \left( \vec{\theta} , z \right)$ とおくと、

$\displaystyle loss \left( \vec{\theta} + \gamma \vec{g} , z \right)=loss \left( \vec{\theta} , z \right) + \gamma \nabla loss \left( \vec{\theta} , z \right) \vec{g} + O\left( \gamma^{2} \right)$

$\displaystyle loss \left( \vec{\theta} + \gamma \vec{g} , z \right) \approx loss \left( \vec{\theta} , z \right) + \gamma \vec{g}^{2}$

一旦、 $\displaystyle \vec{g}^{2}$ ではなく、 $\displaystyle \nabla loss \left( \vec{\theta} , z \right) \vec{g}$ と書いたのは、これが $\displaystyle \vec{g}$ に沿った $\displaystyle　loss \left( \vec{\theta} , z \right)$ の方向微分であることを強調するため。